VI. MATHEMATICAL MODELING OF HYDROGEOLOGICAL CONDITIONS OF KYZYLZHARMINSKI DEPOSIT OF GROUNDWATERS FROM SYRDARYINSKI ARTESIAN BASIN FOR WATER SUPPLY OF THE CITY OF KYZYLORDA
1. Creation of mathematical model of hydrogeological conditions of Kyzylzharminski deposit of groundwaters
As the aim of modeling is economical-potable water supply for the city of Kyzylorda. It has been necessary for this aim to forecast on the model the water levels (levels depressions) and the mineralization of the water taken from existing and projecting water intaking wells for the final data of their exploitation.
Report of A.G.Satpaev, Director of the Institute of hydrogeology and geoecology named of U.M.Akhmedsafin has been dedicated to the problems of quality potable water for the city of Kyzylorda. It was published at the new-paper “Kazakhstanskaya Pravda” on March, 2011 (in Russian).
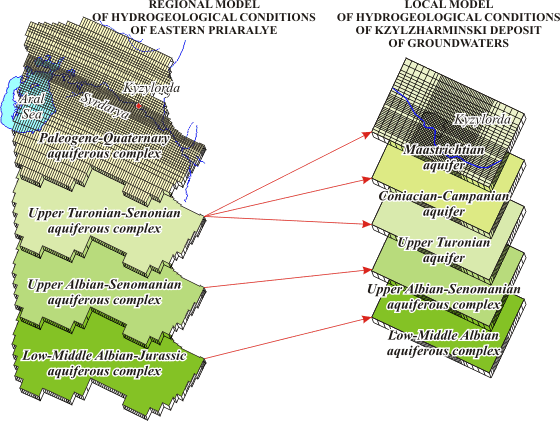
Models systems structure and regional model layers correlation of Eastern Priaralye and those of local model of Kyzylzharminski deposit of groundwaters
|
Groundwaters on investigable territory are confined to the Quaternary, Neogenic and Cretaceous deposits. Groundwaters of Quaternary and Neogenic deposits are subjected to pollution and cannot be safe source of economical potable water supply for the city of Kyzylorda. They are divided from occurring below Cretaceous clays by thick cover of water-resisting Paleogene clays; the overflowing through which is practically absent and it cannot be taken in consideration.
Cretaceous aquifers and aquiferous complexes are divided among themselves by weakly-permeable clayish deposits, through which the groundwaters overflow is possible. The Upper-Turonian aquifer is the most perspective for utilization. Influence of existing and projected operating wells onto groundwaters state has been taken into consideration during modeling.
Programming complex GMS 6.0 has been used for modeling.
Mathematical model of Kyzylzharminski groundwaters deposit was been creating as the local model incoming together with regional model of Eastern Priaralye, into the system of inter connected variously scaled mathematical models.
|
| Hydrogeological conditions in plan have been schematized in the form of rectangular region with size of 61.3 x 50 km, in the centre of which are situated existing and projected wells exploiting groundwaters of Upper-Turonian aquifer of Kyzylzharminski deposit. The region modeled in plan is approximated by orthogonal grid with size MxN = 143x122, the step of which is changing from 250 m in central part and to 750 m as of periphery of the model. Configuration of the grid and its position in space was selected by such a way that at the corners of model and in the separate points through its outer border the nodes of the grid were coinciding with nodes of the grid at the regional model of Eastern Priaralye.
During hydrogeological conditions schematization in section it has been taken into consideration that one of the aims of modeling was groundwaters quality change forecast. Therefore it has been taken the decision concerning of the three- dimensional model preparation. The section is schematized in the form of five head water permeable layers divided by three weakly permeable layers. One block was corresponding to each permeable layer on the model in section, and to each weakly permeable layer – three blocks.
Water intaking wells were assigned on the model as discharges changing in time.
| Hydrogeological conditions schematization in section
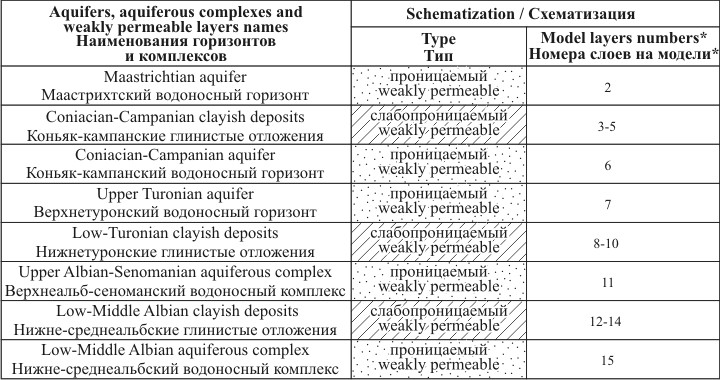
* Ñëîé ¹1 ìîäåëè ñîîòâåòñòâóåò íåïðîíèöàåìûì ïàëåîãåíîâûì ãëèíàì
* Layer ¹ 1 of the model corresponds to impermeable Paleogene clays
|
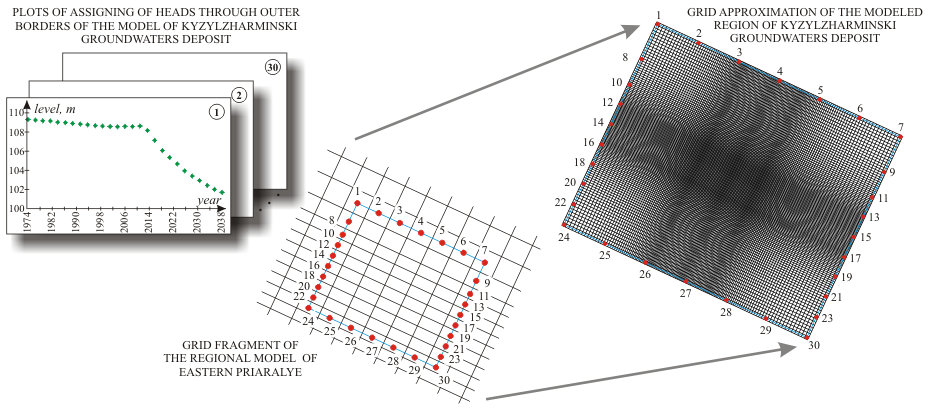
|
During solution of reverse stationary task as of outer boundaries of all the aquifers and aquiferous complexes, boundary conditions of the first order (changing in time head) were assigned. During solution of epignostic and prognostic tasks as of the borders of Maastrichtian aquifer, constant in time groundwaters flow discharge has been assigned which has been calculated from the results of stationary task solution. Boundary conditions of the first order have been assigned in outer borders of all the other aquifers and aquiferous complexes.
Absolute marks of the levels, assignable through outer borders of the first order were calculated with taking into consideration of levels depressions, calculated in the corresponding blocks of regional model of Eastern Priaralye.
|
Geofiltration processes schematization
The three-dimensional steady movement of ground water of constant density through porous earth material may be described by the partial-differential equation
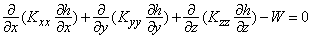
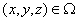
with boundary conditions
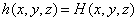
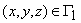
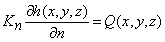
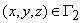
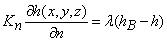
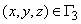
where Kxx, Kyy, Kzz are values of hydraulic conductivity along the x, y, z coordinate axes, which are assumed to be parallel to the major axes of hydraulic conductivity (LT-1);
h is the potentiometric head (L);
W is a volumetric flux per unit volume and represents sources and/or sinks of water (T-1).
In general, Kxx, Kyy, Kzz, W may be functions of space (Kxx(x,y,z), etc.).
 is the modeled area,
is the modeled area,
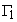 is the specified head boundary,
H(x,y,z) is the head along the boundary
is the specified head boundary,
H(x,y,z) is the head along the boundary 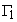 ;
;
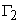 is the given water discharge boundary,
Kn is the values of hydraulic conductivity as of normal to boundary,
Q(x,y,z) is the water discharge per unit volume;
is the given water discharge boundary,
Kn is the values of hydraulic conductivity as of normal to boundary,
Q(x,y,z) is the water discharge per unit volume;
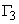 is the boundary along which the dependence between water discharge and head gradient is given;
is the boundary along which the dependence between water discharge and head gradient is given;
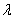 is a factor characterizing the interrelation with the outer filtrational environment,
hB is the head in the outer filtrational environment.
is a factor characterizing the interrelation with the outer filtrational environment,
hB is the head in the outer filtrational environment.
The three-dimensional unsteady movement of ground water of constant density through porous earth material may be described by the partial-differential equation
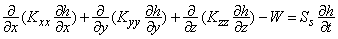
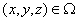
with initial conditions
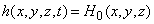
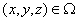 ,
, 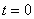
with boundary conditions
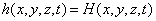
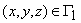 ,
, 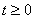
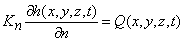
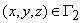 ,
, 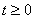
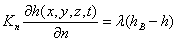
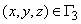 ,
, 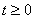
where Kxx, Kyy, Kzz are values of hydraulic conductivity along the x, y, z coordinate axes, which are assumed to be parallel to the major axes of hydraulic conductivity (LT-1);
h is the potentiometric head (L);
W is a volumetric flux per unit volume and represents sources and/or sinks of water (T-1);
Ss is the specific storage of the porous material (L-1);
t is time (T).
In general, Ss, Kxx, Kyy, Kzz may be functions of space ( Ss= Ss (x,y,z), K xx (x,y,z) ,etc.) and
W may be a function of space and time (W= W(x,y,z,t)).
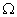 is the modeled area,
H0(x,y,z) is the known head distribution of the initial time moment;
is the modeled area,
H0(x,y,z) is the known head distribution of the initial time moment;
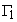 is the specified head boundary,
H(x,y,z,t) is the head along the boundary
is the specified head boundary,
H(x,y,z,t) is the head along the boundary 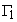 ;
;
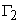 is the given water discharge boundary,
Kn is the values of hydraulic conductivity as of normal to boundary,
Q(x,y,z,t) is the water discharge per unit volume;
is the given water discharge boundary,
Kn is the values of hydraulic conductivity as of normal to boundary,
Q(x,y,z,t) is the water discharge per unit volume;
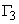 is the boundary along which the dependence between water discharge and head gradient is given,
is the boundary along which the dependence between water discharge and head gradient is given,
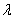 is a factor characterizing the interrelation with the outer filtrational environment,
hB is the head in the outer filtrational environment.
is a factor characterizing the interrelation with the outer filtrational environment,
hB is the head in the outer filtrational environment.
The partial differential equation describing the transport of contaminants of species k in 3-D, transient groundwater flow systems can be written as follows
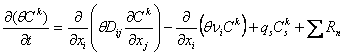
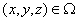
with initial conditions
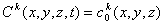
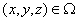 ,
, 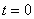
with boundary conditions
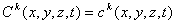
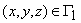 ,
, 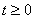
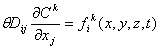
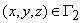 ,
, 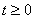
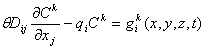
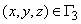 ,
, 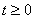
where Ck is the dissolved concentration of species k (ML-3);
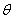 is the porosity of the subsurface medium (dimensionless);
t is a time;
xi is the distance along the respective Cartesian coordinate axis (L);
Dij is the hydrodynamic dispersion coefficient tensor (L2T-1);
is the porosity of the subsurface medium (dimensionless);
t is a time;
xi is the distance along the respective Cartesian coordinate axis (L);
Dij is the hydrodynamic dispersion coefficient tensor (L2T-1);
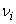 is the seepage or linear pore water velocity (LT-1), it is related to the specific discharge or Darcy flux through the relationship
is the seepage or linear pore water velocity (LT-1), it is related to the specific discharge or Darcy flux through the relationship 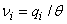 ;
qs is the volumetric flow rate per unit volume of aquifer representing fluid sources (positive) and sinks (negative) (T-1);
;
qs is the volumetric flow rate per unit volume of aquifer representing fluid sources (positive) and sinks (negative) (T-1);
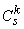 is the concentration of the source or sink flux for species k (ML-3);
is the concentration of the source or sink flux for species k (ML-3);
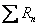 is the chemical reaction term (sorption, radioactive decay or biodegradation processes) (L-3T-1).
is the chemical reaction term (sorption, radioactive decay or biodegradation processes) (L-3T-1).
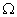 is the modeled area;
is the modeled area;
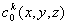 is the known concentration distribution at the initial time moment;
is the known concentration distribution at the initial time moment;
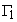 is the specified concentration boundary,
ck(x,y,z,t) is the given concentration along boundary
is the specified concentration boundary,
ck(x,y,z,t) is the given concentration along boundary 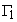 ;
;
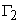 is the boundary with given flow at the expense of dispersion,
is the boundary with given flow at the expense of dispersion,
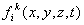 is the dispersive flux by normal to the boundary
is the dispersive flux by normal to the boundary 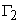 ;
;
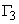 is the boundary along which the interaction between hydrogeological object and environment is occurred,
is the boundary along which the interaction between hydrogeological object and environment is occurred,
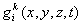 is the total flux (dispersive and advective) by normal to the boundary
is the total flux (dispersive and advective) by normal to the boundary 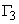 .
.
|
|
 |
Next |



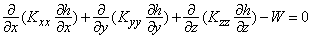
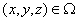
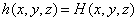
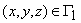
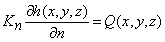
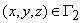
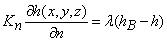
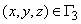
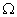 is the modeled area,
is the modeled area,
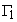 is the specified head boundary,
H(x,y,z) is the head along the boundary
is the specified head boundary,
H(x,y,z) is the head along the boundary 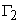 is the given water discharge boundary,
Kn is the values of hydraulic conductivity as of normal to boundary,
Q(x,y,z) is the water discharge per unit volume;
is the given water discharge boundary,
Kn is the values of hydraulic conductivity as of normal to boundary,
Q(x,y,z) is the water discharge per unit volume;
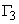 is the boundary along which the dependence between water discharge and head gradient is given;
is the boundary along which the dependence between water discharge and head gradient is given;
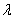 is a factor characterizing the interrelation with the outer filtrational environment,
hB is the head in the outer filtrational environment.
is a factor characterizing the interrelation with the outer filtrational environment,
hB is the head in the outer filtrational environment.
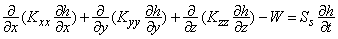
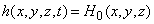
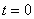
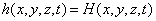
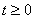
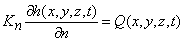
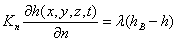
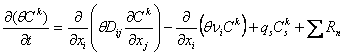
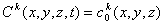
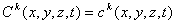
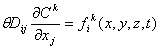
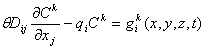
 is the porosity of the subsurface medium (dimensionless);
t is a time;
xi is the distance along the respective Cartesian coordinate axis (L);
Dij is the hydrodynamic dispersion coefficient tensor (L2T-1);
is the porosity of the subsurface medium (dimensionless);
t is a time;
xi is the distance along the respective Cartesian coordinate axis (L);
Dij is the hydrodynamic dispersion coefficient tensor (L2T-1);
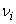 is the seepage or linear pore water velocity (LT-1), it is related to the specific discharge or Darcy flux through the relationship
is the seepage or linear pore water velocity (LT-1), it is related to the specific discharge or Darcy flux through the relationship 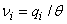 ;
qs is the volumetric flow rate per unit volume of aquifer representing fluid sources (positive) and sinks (negative) (T-1);
;
qs is the volumetric flow rate per unit volume of aquifer representing fluid sources (positive) and sinks (negative) (T-1);
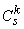 is the concentration of the source or sink flux for species k (ML-3);
is the concentration of the source or sink flux for species k (ML-3);
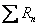 is the chemical reaction term (sorption, radioactive decay or biodegradation processes) (L-3T-1).
is the chemical reaction term (sorption, radioactive decay or biodegradation processes) (L-3T-1).
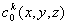 is the known concentration distribution at the initial time moment;
is the known concentration distribution at the initial time moment;
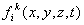 is the dispersive flux by normal to the boundary
is the dispersive flux by normal to the boundary 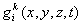 is the total flux (dispersive and advective) by normal to the boundary
is the total flux (dispersive and advective) by normal to the boundary 