VI. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ГИДРОГЕОЛОГИЧЕСКИХ УСЛОВИЙ КЫЗЫЛЖАРМИНСКОГО МЕСТОРОЖДЕНИЯ ПОДЗЕМНЫХ ВОД СЫРДАРЬИНСКОГО АРТЕЗИАНСКОГО БАССЕЙНА ДЛЯ ВОДОСНАБЖЕНИЯ Г.КЫЗЫЛОРДЫ
1. Создание математической модели гидрогеологических условий Кызылжарминского месторождения подземных вод
Целью моделирования являлось решение задачи хозяйственно-питьевого водоснабжения г.Кызылорды. Для достижения этой цели необходимо было спрогнозировать на модели уровни воды (понижения уровней) и минерализацию отбираемой воды в существующих и проектируемых водозаборных скважинах на конечный срок их эксплуатации.
Вопросам снабжения г.Кызылорды качественной питьевой водой было посвящено выступление А.Г.Сатпаева, директора Института гидрогеологии и геоэкологии им.У.М.Ахмедсафина, опубликованное в газете «Казахстанская правда» 15 марта 2011 года.
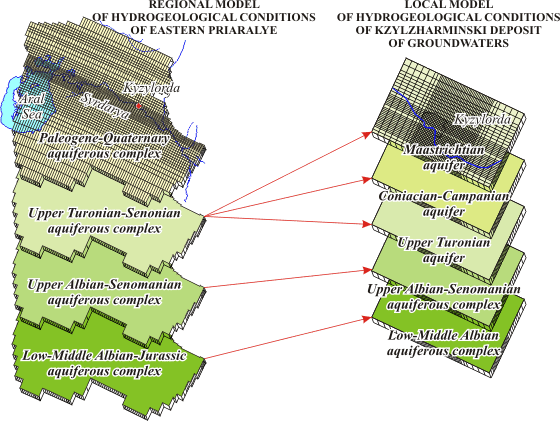
Структура системы моделей и соотношение слоев региональной модели Восточного Приаралья и локальной модели Кызылжарминского месторождения подземных вод
|
На исследуемой территории подземные воды приурочены к четвертичным, неогеновым и меловым отложениям. Подземные воды в четвертичных и неогеновых отложениях подвержены загрязнению и не могут быть надежным источником хозяйственно-питьевого водоснабжения г.Кызылорды. От залегающих ниже меловых водоносных горизонтов они отделены мощной толщей водоупорных палеогеновых глин, перетекание через которые практически отсутствует и им можно пренебречь.
Меловые водоносные горизонты и комплексы разделены между собой слабопроницаемыми глинистыми отложениями, через которые возможно перетекание подземных вод. Наиболее перспективным для использования является верхнетуронский водоносный горизонт. При моделировании учитывалось влияние на состояние подземных вод существующих и проектируемых эксплуатационных скважин.
Для моделирования был использован программный комплекс GMS 6.0.
Математическая модель Кызылжарминского месторождения подземных вод создавалась как локальная модель, входящая вместе с региональной моделью Восточного Приаралья в систему взаимосвязанных разномасштабных математических моделей.
|
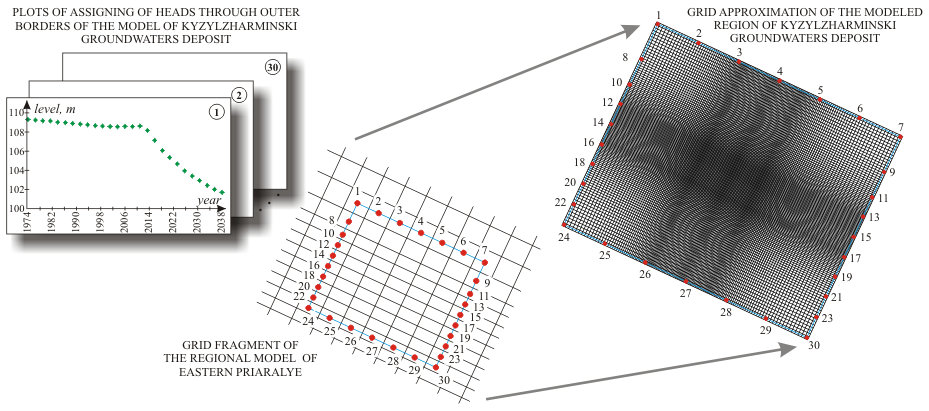
| Гидрогеологические условия в плане были схематизированы в виде прямоугольной области размером 61.3 x 50 км, в центральной части которой располагаются все существующие и проектируемые скважины, эксплуатирующие подземные воды верхнетуронского водоносного горизонта Кызылжарминского месторождения. Моделируемая область в плане аппроксимирована ортогональной неравномерной сеткой размером M x N =143 х 122, шаг которой изменяется от 250 м в центральной части области до 750 м по периферии модели. Конфигурация сети и ее положение в пространстве было выбрано так, что в углах модели и в отдельных точках по ее внешней границе узлы сетки совпадали с узлами сетки региональной модели Восточного Приаралья.
При схематизации гидрогеологических условий в разрезе учитывалось, что одной из целей моделирования является прогнозирование изменения качества подземных вод. Поэтому было принято решение о создании трехмерной модели. Разрез схематизирован в виде пяти напорных водопроницаемых слоев, разделенных тремя слабопроницаемыми. Каждому проницаемому слою на модели в разрезе соответствовал один блок, а каждому слабопроницаемому – три.
Водозаборные скважины задавались на модели как стоки с изменяющимся во времени расходом.
| Схематизация гидрогеологических условий в разрезе
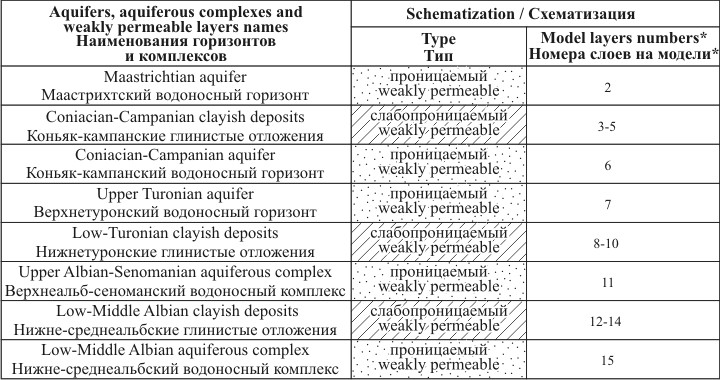
* Слой №1 модели соответствует непроницаемым палеогеновым глинам
* Layer № 1 of the model corresponds to impermeable Paleogene clays
|
|
При решении обратной стационарной задачи по внешним границам всех водоносных горизонтов и комплексов задавались граничные условия I рода (изменяющийся во времени напор). При решении эпигнозной и прогнозной задач по границам маастрихтского водоносного горизонта задавался постоянный во времени расход потока подземных вод, который рассчитывался по результатам решения стационарной задачи. По внешним границам всех остальных водоносных горизонтов и комплексов задавались граничные условия I рода.
Абсолютные отметки уровней, задаваемых по внешним границам I рода, рассчитывались с учетом понижений уровней, вычисленных в соответствующих блоках региональной модели Восточного Приаралья.
|
Схематизация процессов геофильтрации
Трехмерная стационарная фильтрация потока подземных вод в гетерогенной и анизотропной среде в общем случае описывается уравнением
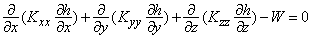
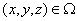
с граничными условиями
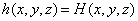
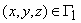
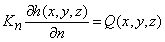
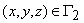
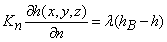
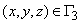
где Kxx, Kyy, Kzz – коэффициенты фильтрации по направлению координатных осей x, y, z (LT-1); h – напор (L); W – объемный поток на единицу объема, представляет источники и/или стоки воды (T-1). В общем случае функции Kxx, Kyy, Kzz, W могут быть функциями пространственных координат (Kxx(x,y,z) и т.д.).
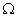 – моделируемая область,
– моделируемая область, 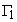 – граница с заданным напором, H(x,y,z) – значение напора вдоль границы
– граница с заданным напором, H(x,y,z) – значение напора вдоль границы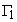 ;
; 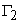 – граница с заданным расходом воды, Kn – коэффициент фильтрации по нормали к границе, Q(x,y,z) – расход воды на единицу объема;
– граница с заданным расходом воды, Kn – коэффициент фильтрации по нормали к границе, Q(x,y,z) – расход воды на единицу объема; 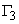 - граница, вдоль которой задана зависимость между расходом воды и градиентом напора;
- граница, вдоль которой задана зависимость между расходом воды и градиентом напора; 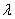 – коэффициент, характеризующий взаимосвязь с внешней фильтрационной средой, hB – уровень воды во внешней фильтрационной среде.
– коэффициент, характеризующий взаимосвязь с внешней фильтрационной средой, hB – уровень воды во внешней фильтрационной среде.
Трехмерная нестационарная фильтрация потока подземных вод в гетерогенной и анизотропной среде в общем случае описывается уравнением
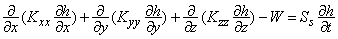
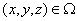
с начальными условиями
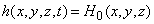
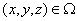 ,
, 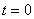
с граничными условиями
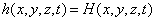
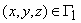 ,
, 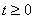
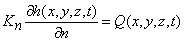
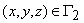 ,
, 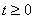
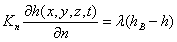
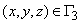 ,
, 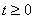
где Kxx, Kyy, Kzz – коэффициенты фильтрации по направлению координатных осей x, y, z (LT-1); h – напор (L); W – объемный поток на единицу объема, представляет источники и/или стоки воды (T-1);
Ss - коэффициент водоотдачи пористого материала (L-1); t – время (T).
В общем случае функции Ss, Kxx, Kyy, Kzz могут быть функциями пространственных координат ( Ss= Ss (x,y,z), K xx (x,y,z) и т.д.) и W - функцией пространственных координат и времени (W= W(x,y,z,t)).
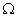 – моделируемая область,
H0(x,y,z) - известное распределение напора в начальный момент времени;
– моделируемая область,
H0(x,y,z) - известное распределение напора в начальный момент времени;
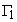 – граница с заданным напором,
H(x,y,z,t) – значение напора вдоль границы
– граница с заданным напором,
H(x,y,z,t) – значение напора вдоль границы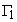 ;
; 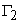 – граница с заданным расходом воды, Kn – коэффициент фильтрации по нормали к границе, Q(x,y,z,t) – расход воды на единицу объема;
– граница с заданным расходом воды, Kn – коэффициент фильтрации по нормали к границе, Q(x,y,z,t) – расход воды на единицу объема; 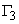 - граница, вдоль которой задана зависимость между расходом воды и градиентом напора;
- граница, вдоль которой задана зависимость между расходом воды и градиентом напора; 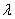 – коэффициент, характеризующий взаимосвязь с внешней фильтрационной средой, hB – уровень воды во внешней фильтрационной среде.
– коэффициент, характеризующий взаимосвязь с внешней фильтрационной средой, hB – уровень воды во внешней фильтрационной среде.
Математическая модель переноса потоком подземных вод растворенных в них компонентов в общем случае описывается уравнением
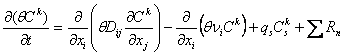
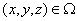
с начальными условиями
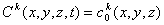
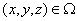 ,
, 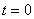
с граничными условиями
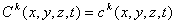
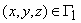 ,
, 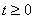
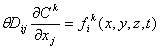
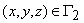 ,
, 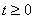
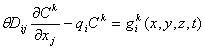
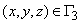 ,
, 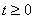
где Ck – концентрация растворенного k-го компонента (ML-3);
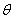 – пористость фильтрационной среды, безразмерная величина;
t – время;
xi – координата, соответствующая i-ой декартовой оси координат, (L);
Dij – тензор коэффициента гидродинамической дисперсии (L2T-1);
– пористость фильтрационной среды, безразмерная величина;
t – время;
xi – координата, соответствующая i-ой декартовой оси координат, (L);
Dij – тензор коэффициента гидродинамической дисперсии (L2T-1);
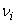 – скорость фильтрации (LT-1), она определяется как поток Дарси через отношение
– скорость фильтрации (LT-1), она определяется как поток Дарси через отношение 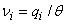 ;
qs – объемный поток на единицу объема водоносного горизонта, представляющий источник (положительный) или сток (отрицательный) (T-1);
;
qs – объемный поток на единицу объема водоносного горизонта, представляющий источник (положительный) или сток (отрицательный) (T-1);
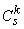 – концентрация растворенного k-го компонента в источнике или стоке (ML-3);
– концентрация растворенного k-го компонента в источнике или стоке (ML-3);
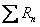 - элемент, отвечающий за химические реакции (сорбцию, радиоактивный распад или процессы биодеградации) (L-3T-1).
- элемент, отвечающий за химические реакции (сорбцию, радиоактивный распад или процессы биодеградации) (L-3T-1).
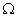 - моделируемая область;
- моделируемая область;
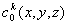 - известное распределение концентрации в начальный момент времени;
- известное распределение концентрации в начальный момент времени;
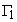 - граница с заданной концентрацией,
ck(x,y,z,t) - значение концентрации по границе
- граница с заданной концентрацией,
ck(x,y,z,t) - значение концентрации по границе 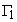 ;
;
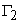 - граница с заданным потоком массы вещества,
- граница с заданным потоком массы вещества,
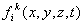 - поток массы по границе
- поток массы по границе 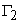 ;
;
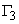 - граница, вдоль которой происходит взаимодействие между гидрогеологическим объектом м окружающей средой,
- граница, вдоль которой происходит взаимодействие между гидрогеологическим объектом м окружающей средой,
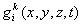 - суммарный поток массы (за счет дисперсии и адвекции) по нормали к границе
- суммарный поток массы (за счет дисперсии и адвекции) по нормали к границе 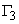 .
.
|
|
 |
Следующая глава |



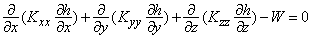
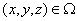
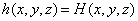
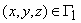
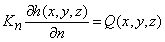
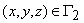
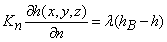
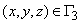
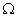 – моделируемая область,
– моделируемая область, 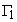 – граница с заданным напором, H(x,y,z) – значение напора вдоль границы
– граница с заданным напором, H(x,y,z) – значение напора вдоль границы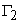 – граница с заданным расходом воды, Kn – коэффициент фильтрации по нормали к границе, Q(x,y,z) – расход воды на единицу объема;
– граница с заданным расходом воды, Kn – коэффициент фильтрации по нормали к границе, Q(x,y,z) – расход воды на единицу объема; 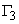 - граница, вдоль которой задана зависимость между расходом воды и градиентом напора;
- граница, вдоль которой задана зависимость между расходом воды и градиентом напора; 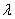 – коэффициент, характеризующий взаимосвязь с внешней фильтрационной средой, hB – уровень воды во внешней фильтрационной среде.
– коэффициент, характеризующий взаимосвязь с внешней фильтрационной средой, hB – уровень воды во внешней фильтрационной среде.
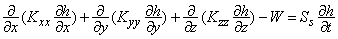
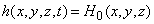
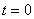
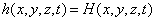
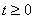
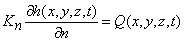
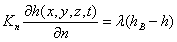
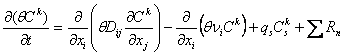
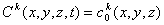
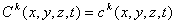
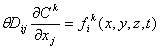
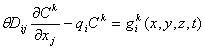
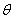 – пористость фильтрационной среды, безразмерная величина;
t – время;
xi – координата, соответствующая i-ой декартовой оси координат, (L);
Dij – тензор коэффициента гидродинамической дисперсии (L2T-1);
– пористость фильтрационной среды, безразмерная величина;
t – время;
xi – координата, соответствующая i-ой декартовой оси координат, (L);
Dij – тензор коэффициента гидродинамической дисперсии (L2T-1);
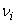 – скорость фильтрации (LT-1), она определяется как поток Дарси через отношение
– скорость фильтрации (LT-1), она определяется как поток Дарси через отношение 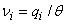 ;
qs – объемный поток на единицу объема водоносного горизонта, представляющий источник (положительный) или сток (отрицательный) (T-1);
;
qs – объемный поток на единицу объема водоносного горизонта, представляющий источник (положительный) или сток (отрицательный) (T-1);
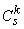 – концентрация растворенного k-го компонента в источнике или стоке (ML-3);
– концентрация растворенного k-го компонента в источнике или стоке (ML-3);
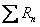 - элемент, отвечающий за химические реакции (сорбцию, радиоактивный распад или процессы биодеградации) (L-3T-1).
- элемент, отвечающий за химические реакции (сорбцию, радиоактивный распад или процессы биодеградации) (L-3T-1).
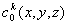 - известное распределение концентрации в начальный момент времени;
- известное распределение концентрации в начальный момент времени;
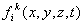 - поток массы по границе
- поток массы по границе 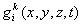 - суммарный поток массы (за счет дисперсии и адвекции) по нормали к границе
- суммарный поток массы (за счет дисперсии и адвекции) по нормали к границе 